#数楽 https://twitter.com/genkuroki/status/775907480819863552 … の続き奥村晴彦著『Rで楽しむ統計』 p.55より【ランダムにお金をやりとりすると、指数分布に近づき、貧富の差は増す】指数分布の確率はe^{-βE}に比例(β>0)。Eはランダムに選んだ個人が保有するお金の量。
#数楽 β>0のとき、個人が保有するお金の量Eの函数e^{-βE}は単調減少函数。Eが小さいほど確率が高い。ランダムにお金をやりとりする世界では貧困の問題がひどくなることを確率論を使って証明できるし、コンピューターシミュレーションでも確認できる。カノニカル分布の話。
#数楽 「ランダムにお金をやりとりを続けるとランダムに選んだ個人が保有するお金の量がEである確率がe^{-βE}に比例するようになる」ことを証明するにはどうしたらよいのだろうか?答えは何度も言及しているSanovの定理である→ http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160616KullbackLeibler.pdf …
#数楽 多項分布を独立なPoisson分布の積の制限(観測度数の総和はnで一定)で表現することができるのと同じように、ランダムにお金をやり取りした結果の確率分布を独立なある確率分布の積の制限(全員が持っているお金の総和が一定)で表現することができる。
#数楽 続き。個人が保有できる金額はE_1,…,E_rのどれかであるとし、一様分布を仮定する。この設定のもとで、U≦ΣE_i/rであると仮定し、n人の保有する金額の平均〈E〉がU以下である場合に確率分布を制限する。するとn→∞で分布は〈E〉≈Uに集中するようになり、続く
#数楽 続き~、ランダムに選んだ個人が保有する金額がE_iである確率はe^{-βE_i}に比例するようになる。比例定数はZ(β)=Σe^{-βE_i}で、βはΣe^{-βE_i}E_i/Z(β)=Uから決まる。証明は http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160616KullbackLeibler.pdf … に書いてある。
#数楽 続き。要するに、nが大きくてかつ、n人のそれぞれが保有する金額がランダム(一様分布)だが、n人全体で保有するお金の合計がある上限以下という制限を付けると、各個人が保有するお金の金額がE_iである確率はe^{-βE_i}に(近似的に)比例するようになってしまうのだ!
#数楽 出発点の分布が一様分布でない場合についても http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160616KullbackLeibler.pdf … で扱っている。お金の総量に制限がない状況で個人が保有するお金の金額がE_iである確率がq_iであるとき、n人が保有するお金の総量をnU以下に制限すると~続く
#数楽 続き~、個人が保有するお金の金額がE_iになる確率は e^{-βE_i}q_i に比例するようになります。n人全体が保有するお金の総量に制限を付けると、個人が保有する金額がE_iになる確率は制限がない場合の確率q_iにe^{-βE_i}をかけたものになるのだ。続く
#数楽 続き。(U≦ΣE_i q_iと仮定。βはΣe^{-βE_i}q_i E_i=U、Z(β)=Σe^{-βE_i}q_iから決まる。)e^{-βE_i}はE_iの単調減少函数なので、ランダムネスの仮定のもとで、お金の総量の制限は貧富の差を拡大するというわけです。続く
#数楽 以上の話の数学的に厳密な証明は技術的にそう難しくありません。所謂、大偏差原理の平易な場合であるSanovの定理の易しいバージョンです。証明の解説は http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160616KullbackLeibler.pdf … にあります。かなりの部分が高校レベルの数学で間に合う。
デフレが貧富の差を拡大した仕組みってもしかしてこれじゃないの?「これ」=「以上で説明した統計力学におけるカノニカル分布の話」=「 http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160616KullbackLeibler.pdf … の第2節と第4節の内容」
#数楽 なるほど、奥村晴彦さんの新著『Rで楽しむ統計』 https://www.amazon.co.jp/dp/4320112415 は奥村さんが収集した現代人が知っておくべき様々な教養を身に付けながら、Rでの統計処理もマスターできるように構成されているか。この本を眺めて興味を持てることが増えたら最高かも。
#数楽 奥村さんのこの本は本文部分だけではなく、✎マークの「註」に当たる部分がすごく面白い。✎マークの分量はかなり多い。✎マークに追い出された事柄についても本気で解説を書きまくったらページ数は数倍に膨れ上がるのではないだろうか?
#数楽 奥村晴彦著『Rで楽しむ統計』https://amazon.co.jp/dp/4320112415 p.138より【そこで、有意でない変数を外していけば、予測式はより安定する。どれくらい良い予測式であるかを評価するための指標はいろいろ考えられるが、ここではAIC~以下略】続く
#数楽 https://twitter.com/genkuroki/status/773005404448043008 … にも書いたことですが、AICの定義は(モデルの予測精度を上げるためには大きくしたい)対数尤度の期待値のn倍の近似値である(標本サイズnでの対数尤度標本平均)-(モデルのパラメーターの個数)の-2倍です。続く
#数学 Sanovの定理から、モデルの予測精度の高さは「KL情報量の小ささ」で評価できます。そして「KL情報量が小さい」⇔「(真の確率分布のもとでの)対数尤度の期待値が大きい」で、対数尤度の期待値はAICの-1/(2n)倍で近似される。AICが小さい方がKL情報量が小さくなる。
#数楽 ここでも、Kullback-Leibler情報量が関係して来る。未知である真の確率分布を定義式の中に含むKL情報量と(真の確率分布のもとでの)対数尤度の期待値は観測された量だけから計算できないのですが、観測された量だけで後者の近似値を得ることはできる。それがAIC。
#数楽 以下の項目はKullback-Leibler情報量とSanovの定理と関係がある。(1)Poisson分布や多項分布や「分割表の確率分布」の中心極限定理(2)ランダムにお金をやりとりしてかつお金の総量に上限があるならば貧富の差が増すこと(3)赤池情報量基準AIC
#数楽 やはり、「大数の法則」と「中心極限定理」の伝統的かつ系統的な利用だけではなく、「Sanovの定理」(Kullback-Leibler情報量もしくは相対エントロピー)も「普通の道具」として利用する方が健全にかつより直観的に様々なことを理解できるように思われます。
#数楽 というわけで、解説ノートを再度紹介http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160616KullbackLeibler.pdf …Kullback-Leibler情報量とSanovの定理

#数楽 添付画像は高橋陽一郎「確率論の広がり」数学のたのしみno.8(1998)pp.26-35の最初のページにある問題。 pic.twitter.com/D1G0yNQAxp(5)がKullback-Leibler情報量=-相対エントロピーとSanovの定理の応用問題です。
#数楽 続き。問題(5)の解説が https://twitter.com/genkuroki/status/741099709285031936 … 以降の連続ツイートにあります。まず二項分布と(相対)エントロピー(-KL情報量)について十分に理解できれば、他は「直観的に以下同様」になります。
#数楽 https://twitter.com/genkuroki/status/775934628980936704 …リンク先のツイート以後の解説を難しくし過ぎた。初等的な議論で示せるので以下で解説します。設定:nは大きいとし、n人のそれぞれがお金を保有しており、n人分の合計金額は一定であり、ランダムにお金をやり取りしまくる。続く
#数楽 訂正版。続き。証明の概略。n人が保有する金額の合計をnUと書く。n人が保有する金額は0以上で、総和はnUになる。可能な場合全体は集合Ω_n(nU)={(E_1,…,E_n)∈Z_{≧}|ΣE_i=nU}で表現される。あとは場合の数を評価する計算になる。続く
#数楽 続き。i番目の人が金額Eを保有することと残りのn-1人が保有する金額の合計がnU-Eであることは同値なので、その場合の数は集合Ω_{n-1}(nU-E)の元の個数に等しい。その個数をΩ_n(nU)で割ればその場合の確率が得られる。続く
#数楽 Ω_n(nU)の元の個数はほぼnUのn-1乗に比例し、Ω_{n-1}(nU-E)の元の個数はほぼnU-Eのn-2乗に比例するので、i番目の人が金額Eを保有している確率はほぼ(nU-E)^{n-2}/(nU)^{n-1}に比例する。これで本質的に議論終了である。続く
#数楽 nが大きくて、EがnUよりずっと小さいならば(nU-E)^{n-2}/(nU)^{n-1}=(nU/(nU-E)^2) (1-E/(nU))^n≈(1/(nU)) e^{-E/U}.i人目が金額E保有する確率はほぼ e^{-E/U} に比例することがわかった。
#数楽 Uは1人あたりが保有する金額の期待値なのだが、確率密度函数 e^{-E/U}/U の確率分布(指数分布と呼ばれる)の期待値もUなのでつじつまは合っています。Uは統計力学における絶対温度に対応しています。個人が保有するお金の平均値←→統計力学における絶対温度
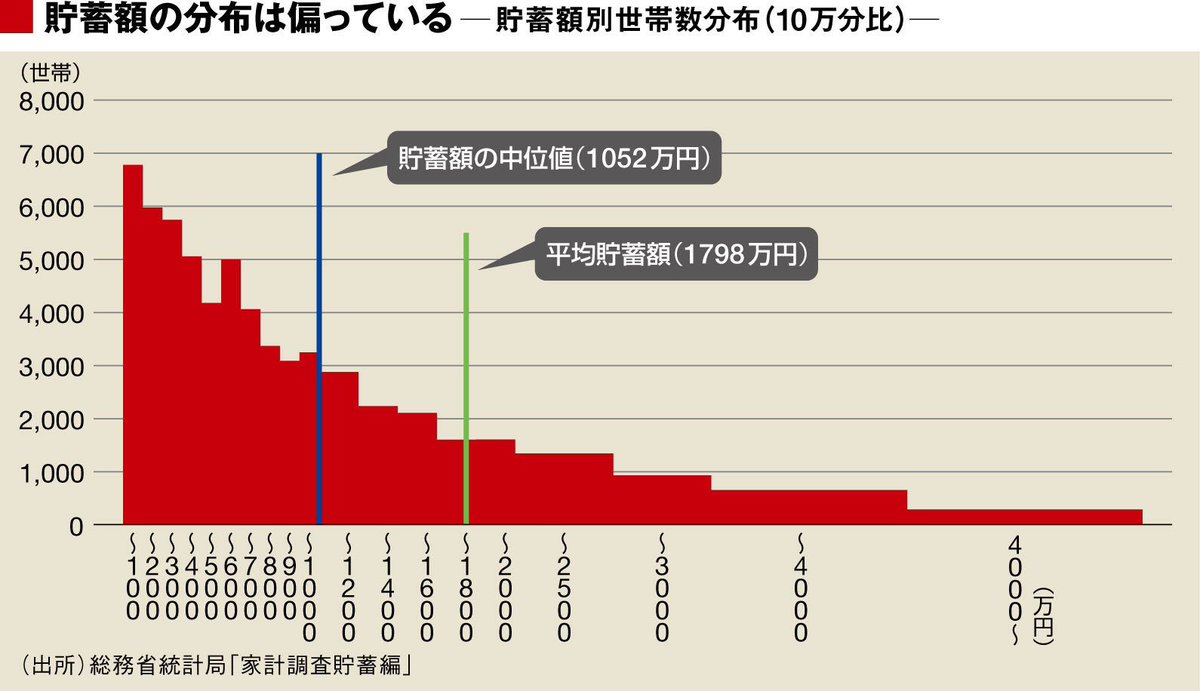
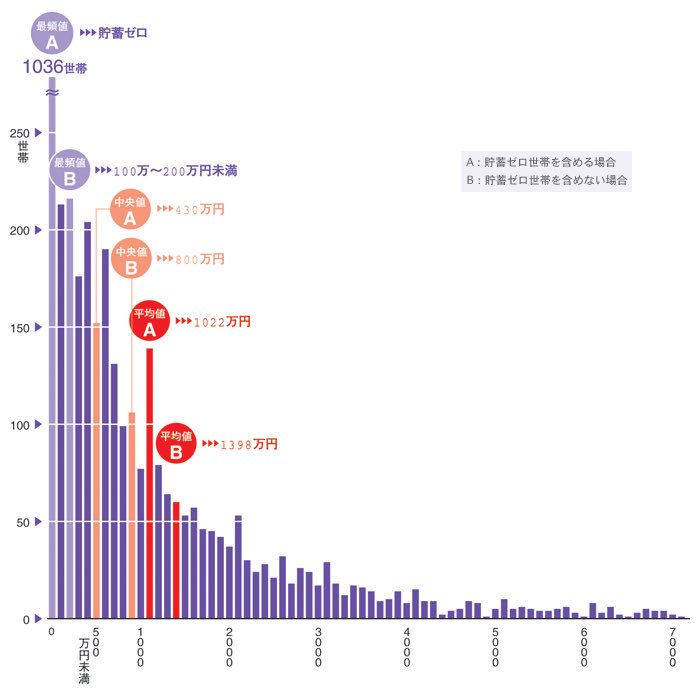
#数楽 現実の資産分布はどうなっているか?このツイートの添付画像は http://toyokeizai.net/articles/-/93693?page=2 … より。pic.twitter.com/5xgUv0Z5Nf

#数楽 指数分布の普遍性を理解してもらうために授業時間に次のような実験をすることが考えられる。(1)出席者におもちゃのお金を配る。全員に同じ金額を配ってもよきし、偏りがあってもよい。(2)ランダムに相手を変えながら、じゃんけん勝負をしてお金をどんどんやりとりしてもらう。続く
#数楽 適当な時刻に、保有しているおもちゃのお金を集計して分布を記録する。十分時間が立つと分布は指数分布に落ち着くことが確認できるはず。物理の授業時間にやってもらえると助かる。
#数楽 上の方で説明した指数分布を出す計算と、R^n内の原点を中心とする半径√(nU)のn-1次元球面上の一様分布を1次元部分空間に射影して得られる分布はn→∞で正規分布に収束するという計算は本質的に同じです。両方の計算をやってみればわかる。「熱浴」の話の簡単な場合。
#数楽 T=σ^2とおく。R^n内の原点を中心とする半径√(nT)の球面上の一様分布を1次元部分空間への射影で得られるR上の確率分布はn→∞で平均0、分散Tの正規分布に収束し、分散Tは統計学における絶対温度に対応します。この話がお金の指数分布の話とほぼ同じなのは明らか。
#数楽 半径√(nT)のn-1次元球面を考えることは、R^nの座標をT=(x_1^2+…+x_n^2)/nと球面上の座標に分解することをやっていると考えられます。以前紹介しましたが、その分解は、PerelmanさんのRiemann幾何的熱浴のアイデアのTaoさんによる解説にも〜
#数楽 続き〜にも登場します。 https://terrytao.wordpress.com/2008/04/27/285g-lecture-9-comparison-geometry-the-high-dimensional-limit-and-perelman-reduced-volume/ … における(9)式を見て下さい。そして(15),(16)式以降の議論を見れば、一様分布の射影の話はラプラス方程式+熱浴から熱方程式を出す議論の一部だと解釈されるべきであることがわかります。
#数楽 総量一定のお金をランダムにやり取りする話(現実世界の貧富の差の問題と関係がある)とポアンカレ予想を解くためのに使われたアイデア(純粋数学の最深部)は地続きで繋がっているのです。下世話に感じられる話は実は下世話ではない。高尚に見える話も単に高尚なわけではない。
#数楽 「熱浴+注目系でのエネルギー保存則より確率がe^{-βE}に比例する」という話は統計力学の教科書に書いてあります。しかし、既出の https://terrytao.wordpress.com/2008/04/27/285g-lecture-9-comparison-geometry-the-high-dimensional-limit-and-perelman-reduced-volume/ … における熱浴+注目系上のラプラス方程式から注目系上の熱方程式を出す議論は見たことがない。
#数楽 大数の法則と中心極限定理はすでに実用的な統計学を習得した人たちにとって空気のようなものになっているのですが、大偏差原理から出て来る話(先の総量が一定のお金のランダムなやりとりで指数分布が自動的に出て来たりする話がその最も簡単な例)についてはそうではないと思う。
#数楽 大偏差原理の取り扱いを知っていれば、統計力学における熱浴のアイデアで、所謂指数型分布族(統計力学におけるカノニカル分布の一般化、正規分布や指数分布を含む)がどのような場合に普遍的に出て来るかがわかります。これも空気のごとくみんなが使えるようになると素晴らしいと思う。
#数楽 総量一定(より正確には1人あたりの量の平均値一定)のお金をたくさんの人たちの間でランダムにやりとりするケースでは、注目する個人意外の人たちが「熱浴」の役目を果たします。奥村さんの新著でも紹介されていたようにこの例は基本的で分かりやすいと思う。
#数楽 注目する個人(もしくはより一般に注目する系)が集団(熱浴)とやりとりするものはお金である必要はなく、なんでもよい。ただし、指数型分布族を出すためには、注目する個人と集団の全体でやりとりするものの総量は一定でなければいけない。たったれだけの条件から〜続く
#数楽 続き。たったこれだけの条件から、個人がやりとりする集団のサイズを大きくする極限でどのような確率分布(指数型分布族に含まれる確率分布になる)に収束するかがわかる。大数の法則や中心極限定理よりも分布の収束先がずっと広く、使用可能なための条件もシンプルでわかり易い。
#数楽 基本定理:ベースになる個人の制限がない場合の分布密度をq(x)とするとき、個人が函数f(x)で表される量をサイズn-1の集団とランダムにやりとりするとき、全体でのf(x)の合計がnUのとき、n→∞で分布密度はe^{-βf(x)}q(x)に比例するようになる。
#数楽 ただし、U≦∫f(x)q(x)dxであるとき、β>0は、Z=∫e^{-βf(x)}q(x)dx、(1/Z)∫f(x)e^{-βf(x)}q(x)dx=Uという条件で決まる。
#数楽 例:総量nUのお金をn人でランダムにやりとりする場合にはM≧Uに対する[0,nM]区間上の一様分布を個人の制限なしの保有するお金xの分布密度と考えます。そして、f(x)=(注目する個人が保有するお金)=x. 結果的に得られる確率分布の密度函数はe^{-βx}に比例。
#数楽 例続き。このとき、Z=∫_0^∞ e^{-βx}dx=1/β、β∫_0^∞ x e^{-βx}dx=1/β=Uなので、β=1/Uとなり、平均Uの指数分布の密度函数e^{-x/U}/Uが得られる。指数分布が普遍的に現れて来る様子がわかります。
#数楽 例:個人ではなく粒子達がエネルギーf(x)=x^2をランダムにやりとりしている場合。n個の粒子全体でエネルギーの総和はnUであるとし、制限を付けないxの分布密度q(x)dxは区間[-√(nU),√(nU)]上の一様分布とする。続く
#数楽 例続き。nを大きくすると注目する粒子のエネルギーの確率密度函数はe^{-βx^2}に比例するようになる。ガウス積分の計算を実行すると、β=1/(2U)、Z=√(2πU)となり、確率密度函数は平均0、分散Uの正規分布になります。続く
#数楽 https://twitter.com/genkuroki/status/776410645046505473 …https://terrytao.wordpress.com/2008/04/27/285g-lecture-9-comparison-geometry-the-high-dimensional-limit-and-perelman-reduced-volume/ … の(6)~(23)の議論は本質的にMaxwell-Boltzman分布の話。ただし、MB分布そのものの話ではなく、次元の大きな調和函数で熱方程式の解を近似できるという話。
#数楽 簡単のため注目する系を1次元とするとMB分布の話は次の公式に要約される。n→∞で∫_{S^{n-1}((y_1,0),√(nt))} f(x_1) dω→∫_R f(x_1) e^{-(x_1-y_1)^2/(2t)}/√(2πt) dx_1ここで~続く
#数楽 続き。ここで、R^n=R×R^{n-1}∋(y_1,0)、S^{n-1}((y_1,0),r)はR^nのおける中心(y_1,0)で半径rの球面、x_1は球面上の点xのR^nの第一成分への射影、dωは球面上の一様分布確率測度。続く
#数楽 続き。左辺は中心(y_1,0)、半径√(nt)のn-1球面上でのf(x_1)の平均で、右辺は平均y_1、分散tの正規分布によるf(x_1)の平均。右辺は熱方程式の解にもなっている。右辺のn→∞での極限が左辺。
#数楽 続き。「無限次元」の調和函数と時間を逆向きにした熱方程式の関係。u=u(t,x)に関する時間の向きを逆転させた熱方程式とはu_t+u_{xx}=0のこと。vが調和函数とはv_{x_1 x_1}+…+v_{x_n x_n}=0を満たすこと。続く
#数楽 u(t,x)からn変数函数vをv(x_1,…,x_n)=u((x_1^2+…+x_n^2)/(2n),x_1)と定めて、vにラプラシアンを作用させるとΔv=u_t+u_{xx}+(x_1/n)u_{tx}+((x_1^2+…+x_n^2)/n^2)u_{tt}.
#数楽 続き。u_t+u_{xx}=0と仮定し、(x_1^2+…+x_n^2)/(2n)=t≦Mに領域を制限し、そこでuおよびその導函数達が有界だとすると、n→∞でΔv=O(1/n)となる。vは次元n→∞で漸近的に調和函数。 https://terrytao.wordpress.com/2008/04/27/285g-lecture-9-comparison-geometry-the-high-dimensional-limit-and-perelman-reduced-volume/ …
#数楽 ラプラシアンの定義はもちろんΔv=v_{x_1 x_1}+…+v_{x_n x_n}です。a_bはaの右下にbと書くことを意味するTeXの書き方で、v_{x_k x_k}はvをx_kで2回偏微分したものを意味している。TeXではひとかたまりにしたい部分を{}で囲む。
#数楽 続き。で、クリアにしたいのは、「Maxwell-Boltzman分布」の話と「熱方程式と"無限次元"調和函数の関係」の話のあいだの関係。どちらも熱浴の話。前者のMB分布の話はクリアに理解できている。後者との関係をまだクリアに理解できている気分になれていない。
#数楽 調和函数は「任意の球面上の平均がその中心での値に一致する」という条件で特徴付けられ、MB分布を出す最も素朴な計算は半径√(nT)のn-1次元球面上の一様分布の射影のn→∞での極限を考えることなので、どちらも球面上での積分(平均)を考える話になっているので当然関係がある。
#数楽 半径√(2nt)のn-1次元球面の方程式は(x_1^2+…+x_n^2)/(2n)=t.これは先の計算中に出て来た式。時間反転熱方程式の解u(t,x)のtにこれとx=x_1を代入してn→∞で漸近的に調和函数になるのであった(無限次元の極限で調和函数)。
#数楽 時間が逆転していると色々間違いそうなので、これ以後は通常の熱方程式を考えることにし、正規分布の分散を時間変数に取りたいので、u=u(t,x)は2u_t=u_{xx}を満たしていると仮定する。基本解は分散tの正規分布e^{-(x-y)^2/(2t)}/√(2πt)。
#数楽 熱方程式の時間発展はu(s+t,y)=∫_R u(s,x) e^{-(x-y)^2/(2t)}/√(2πt) dxなので、s=-tとおくとu(0,y)=∫_R u(-t,x) e^{-(x-y)^2/(2t)}/√(2πt) dx.ここで時間の向きが逆転している?
#数楽 v=v(x_1,…,x_n):=u(-(x_1^2+…+x_n^2)/n,x_1)がn→∞で漸近的に調和函数であることを示すためには中心a半径rの球面上の一様分布測度dωについて∫_{S^{n-1}(a,r)} v dω = v(a)+O(1/n)を出せばよい。
#数楽 メモ:「熱浴」的議論の例の追加一意復号可能符号における符号語長に関するマクミランの不等式Google→ https://www.google.co.jp/search?q=�%83�クミランの不等式+OR+"Mcmillan+inequality" …解説例→ http://www.ide.titech.ac.jp/~yamasita/CN/lecNote/lec08-.pdf …
#数楽 解説符号化の定義域:q個の文字s_1,…,s_qを並べてできる語全体の集合S^*符号化の値域:r個の文字t_1,…,t_rを並べてできる語全体の集合T^*符号化:各s_iごとに1文字以上のw_i∈T^*を対応させることによって構成された写像C:S^*→T^*
#数楽 続き定理(マクミランの不等式)Cは単射(一意復号可能)であると仮定し、各C(s_i)=w_i∈T^*の語としての長さをl_i>0と書くと、Σr^{-l_i}≦1.証明:K=Σr^{-l_i}とおく(iは1からqまでを動く)。K≦1を示せばよい。続く
#数楽 証明続き。l_1,…,l_qの最大値をlと書き、正の整数nに対して、l_{i_1}+…+l_{i_n}=jとなるs=s_{i_1}…s_{i_n}全体の個数をN_jと書くと、K^n=Σ_{j=1}^{nl} N_j r^{-j}.続く
#数楽 証明続き上の記号のもとでw=C(s)はr種類の文字をj個並べたものになる。そのようなwの個数はr^j個以下である。Cの単射せいより、N_j≦r^j. ゆえにK^n=Σ_{j=1}^{nl} N_j r^{-j}≦Σ_{j=1}^{nl} 1=nl.続く
#数楽 証明続きしたがって、K≦(nl)^{1/n}=e^{(1/n)log(nl)}→e^0=1.これでK≦1が示された。 q.e.d.K≦1を直接示すのではなく、K^n≦nlを示すことによって間接的にK≦1を示すところが「熱浴的議論」に見える。
#数楽 私による熱浴関係のツイートは http://twilog.org/genkuroki/search?word=熱浴&ao=a … 経由(返答連鎖をたどる必要あり)でまとめ読みできます。
#数楽 Weil予想でも、Xに関する|α|≦q^{d/2}を直接証明するのではなく、任意のXに関する|α|≦q^{(d+1)/2}から、X^nに関する|α^n|≦q^{(nd+1)/2}を得て、|α|≦q^{(d+1/n)/2}のn→∞での極限で|α|≦q^{d/2}示す方針。
#数楽 訂正https://twitter.com/genkuroki/status/781373228480536576 …「q個の文字s_1,…,s_qを並べてできる語」はより正確には「q種類の互いに異なる文字s_1,…,s_qを重複を許して並べてできる語」。T^*の定義についても同様。
#数楽 以上のq,rを以下ではそれぞれr,bと書き、iは1からrまで動くとする。p_i,q_i>0でそれぞれの総和は1であるとする。Gibbsの情報不等式: Σp_i log(p_i/q_i)≧0.証明はf(x)=x log x にJensenの不等式を適用すれば瞬殺。
#数楽 a_i>0, Σa_i=a≦1のとき、q_i=a_i/aとおいて、Gibbsの情報不等式を使うと、Σp_i log(p_i/a_i)≧-log a≧0となる。すなわち、(*) Σp_i log a_i ≦ Σp_i log p_i.対数の底は任意のb>1でOK.
#数楽 続き。マクミランの不等式より、Σb^{-l_i}≦1なので(先のrをbと書いた)、不等式(*)よりΣp_i l_i≧-Σp_i log_b p_i.左辺は確率分布p_iの下での符号C(s_i)=w_iの長さの平均値で右辺は確率分布p_iのエントロピー。
#数楽 続き。Gibbsの情報不等式Σp_i log(p_i/q_i)≧0の左辺はKullback-Leibler情報量と呼ばれている。対数の底はどのようなb>1であってもよい。対数の底bが符号化に使う文字の種類の個数だとすると、-log q_iは符号長だと解釈可能。続く
#数楽 続き。以上をまとめると、KL情報量Σp_i(-log q_i)-(Σp_i(-log p_i))は確率分布p_iのソースから来る記号をq_iで符号化したときの符号長の平均値がソースのエントロピーよりもどれだけ大きいかを表しているとみなせます。続く
#数楽 続き。マクミランの不等式の逆(クラフトの不等式の逆)より、最短の符号化はソースの確率分布に対応するものになり、その平均符号長はソースのエントロピーになります(少し大雑把な言い方)。だからKL情報量はq_iによる符号化によってどれだけ無駄に符号が必要になるかを意味している。
#数楽 たぶん、渡辺澄夫さんによるカルバック・ライブラ擬距離の解説 http://watanabe-www.math.dis.titech.ac.jp/users/swatanab/klinf.html … (iPhoneならドルフィンブラウザで文字化けせずに読める)は以上のようなことを言いたいのだと思います。
#数楽 Kullback-Leibler情報量には以上とは異なる解釈もあります。それがSanovの定理→ http://www.math.tohoku.ac.jp/~kuroki/LaTeX/20160616KullbackLeibler.pdf … 。素朴には多項分布における確率のn→∞での漸近挙動を見ればKL情報量は自然に出て来る。
#数楽 たぶん「KL情報量が何を意味しているか」を理解するためにはSanovの定理を理解することが最も易しい。確率分布q_iのn回の独立試行によって経験分布p_iが得られる確率はexp(-nΣp_i log(p_i/q_i)+O(log n))の形になります。続く
#数楽 リンクメモ調和振動子に作用させた熱浴のエルゴード性 by @kaityo256 on @Qiita http://qiita.com/kaityo256/items/2b14d7093c43eb5f77d7 …
私見ではNose-Hooverのように決定論的な方法よりもLangevinのほうが「熱浴らしい」と思う。分子動力学の人はわりとLangevinを嫌うみたいだけど。特にダイナミクスを扱いたい場合、決定論的な熱浴は何をやってるのかよくわからないhttps://twitter.com/genkuroki/status/844915902076223489 …



